| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
SYMAXIS - Osie symetrii |
Dla danego zbioru punktów P na płaszczyźnie, odwzorowanie różnowartościowe f: P -> P nazywamy symetrią lustrzaną, jeżeli wszystkie odcinki o końcach (p, f(p)) mają wspólną symetralną, zwaną osią symetrii. Należy wyznaczyć osie symetrii odpowiadające wszystkim symetriom lustrzanym zbioru P.
Wejście
Wejście rozpoczyna się od liczby punktów n (2 <= n <= 105). W kolejnych n liniach podane są przybliżone* współrzędne xi yi poszczególnych punktów ze zbioru P (-1000 < xi, yi < 1000).
Wyjście
W pierwszej linii należy podać współrzędne x y środka ciężkości zbioru, tj. x = (x1+...xn)/n, y = (y1+...yn)/n. W kolejnych liniach należy wypisać wartości kątów ai tworzonych przez poszczególne osie symetrii z osią OX (0< ai <= 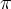 ), uporządkowane rosnąco. Dopuszczalny błąd bezwzględny wypisywanych wartości, modulo
), uporządkowane rosnąco. Dopuszczalny błąd bezwzględny wypisywanych wartości, modulo 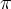 , wynosi 10-6.
, wynosi 10-6.
* Uwaga. Należy przyjmować, że symetria lustrzana występuje, jeżeli można ją dokładnie osiągnąć po skorygowaniu każdej z wartości xi, yi o nie więcej niż pewną wartość graniczną e. Dane testowe są dobrane w taki sposób, że poprawny wynik uzyskuje się dla dowolnej wartości e, 10-9< e < 10-6.
Przykład
Wejście: 10 0.0000000000 10.0000000000 9.5105651630 3.0901699437 5.8778525229 -8.0901699437 -5.8778525229 -8.0901699437 -9.5105651630 3.0901699437 11.7557050458 -16.1803398875 -11.7557050458 -16.1803398875 -19.0211303259 6.1803398875 0.0000000000 20.0000000000 19.0211303259 6.1803398875 Wyjście: 0.0000000000 0.0000000000 0.3141592654 0.9424777961 1.5707963268 2.1991148575 2.8274333882
Materiał pomocniczy
Graficzny framework do wizualizacji rozwiązań zadania by Rush. Wymagane gcc + SDL.
Walkthrough
Łatwiejszy sposób, złożoność O(n2 log n), max. ok. 8 pkt.
- Korzystając z podanej definicji, znajdujemy środek ciężkości zbioru. Odejmujemy współrzędne środka ciężkości od współrzędnych wszystkich punktów. Teraz wszystkie osie symetrii przechodzą przez punkt (0,0). Jeżeli punkt bardzo bliski (0,0) występuje w zbiorze, pomijamy go, zmniejszając n o 1.
- Dla każdego j, 1<=j<=n, sprawdzamy, czy linia prosta będąca symetralną odcinka (p1, pj) i przechodząca przez punkt (0,0) jest osią symetrii zbioru punktów. W tym celu wyznaczamy jej kąt nachylenia względem osi OX, obracamy zbiór punktów o ten kąt względem punktu (0,0), i sprawdzamy, czy oś OX jest (w przybliżeniu) osią symetrii obróconego zbioru. Jeżeli tak, wypisujemy wspomniany kąt nachylenia osi symetrii do OX.
Nieco dłuższy sposób, złożoność O(n log n), max. 12 pkt.
- Patrz powyżej, punkt 1.
- Sortujemy punkty po odległościach względem punktu (0,0). Dzielimy zbiór punktów na rozłączne podzbiory leżące (w przybliżeniu) na okręgach o środku (0,0). Następnie wszystkie te podzbiory rozpatrujemy osobno, wyznaczając ich osie symetrii; prosta jest osią symetrii całego zbioru wtedy i tylko wtedy, gdy jest osią symetrii wszystkich rozważanych podzbiorów.
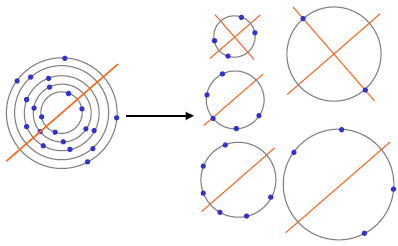
- Procedura wykrywania osi symetrii zbioru punktów leżących na okręgu.
- Obliczamy odległości (najlepiej kątowe) pomiędzy sąsiednimi punktami.
- Wykrywamy te odległości, które są w przybliżeniu identyczne. Nadajemy różnym wartościom odległości etykiety liczbowe (np. 1,...,k) i dalej korzystamy już tylko z tych etykiet.
- Odczytujemy ciąg etykiet na okręgu zgodnie z ruchem wskazówek zegara (S) i przeciwnie do ruchu wskazówek zegara (ST). Każde wystąpienie ST jako podciągu w ciągu S.S (S sklejone z S) definiuje jedną oś symetrii.
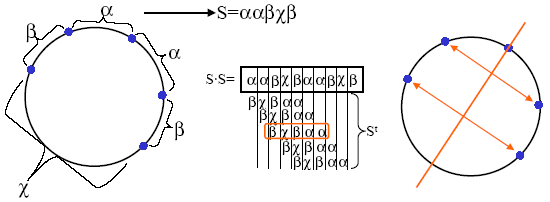 (źródło rysunków)
(źródło rysunków)
Przy rozwiązywaniu pojawia się problem identyfikacji prawie identycznych wartości. Przydatna tu może być intuicja klas abstrakcji z zadania SIMREL (k=10-9).
| Dodane przez: | adrian |
| Data dodania: | 2007-03-03 |
| Limit czasu wykonania programu: | 1s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: GOSU |
| Pochodzenie: | PAL 2007 |
