| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
PYSIM - Python: Symulacja |
Witajcie! Jest to kolejny z serii tutoriali uczący Pythona, a w przyszłości być może nawet Cythona i Numby. Jeśli chcesz nauczyć się nowych, zaawansowanych konstrukcji to spróbuj rozwiązać kilka następnych zadań. Powodzenia!
Symulacje numeryczne pozwalają rozwiązywać problemy, których nie potrafimy rozwiązać analitycznie. Pamiętacie jak wujek Stanisława Ulama grywał w kasynie Monte Carlo? Ulam i von Neumann zastosowali symulacje numeryczne do rozwiązania problemu przy budowie pierwszej bomby nuklearnej. Od tamtego czasu symulacje numeryczne są powszechnie używanym narzędziem. W tym zadaniu zastosujemy symulację do obliczenia obszaru nad jakim spadną odłamki eksplodującej rakiety.
Zakładam że umiesz już posługiwać się tablicami w numpy'u. Jeśli nie, lepiej powróć do poprzednich zadań. W tym zadaniu będziesz potrzebował wielu z metod numpy'a. Wszystkie funkcje są dostępne w dokumentacji w zakładce Routines.
Zadanie
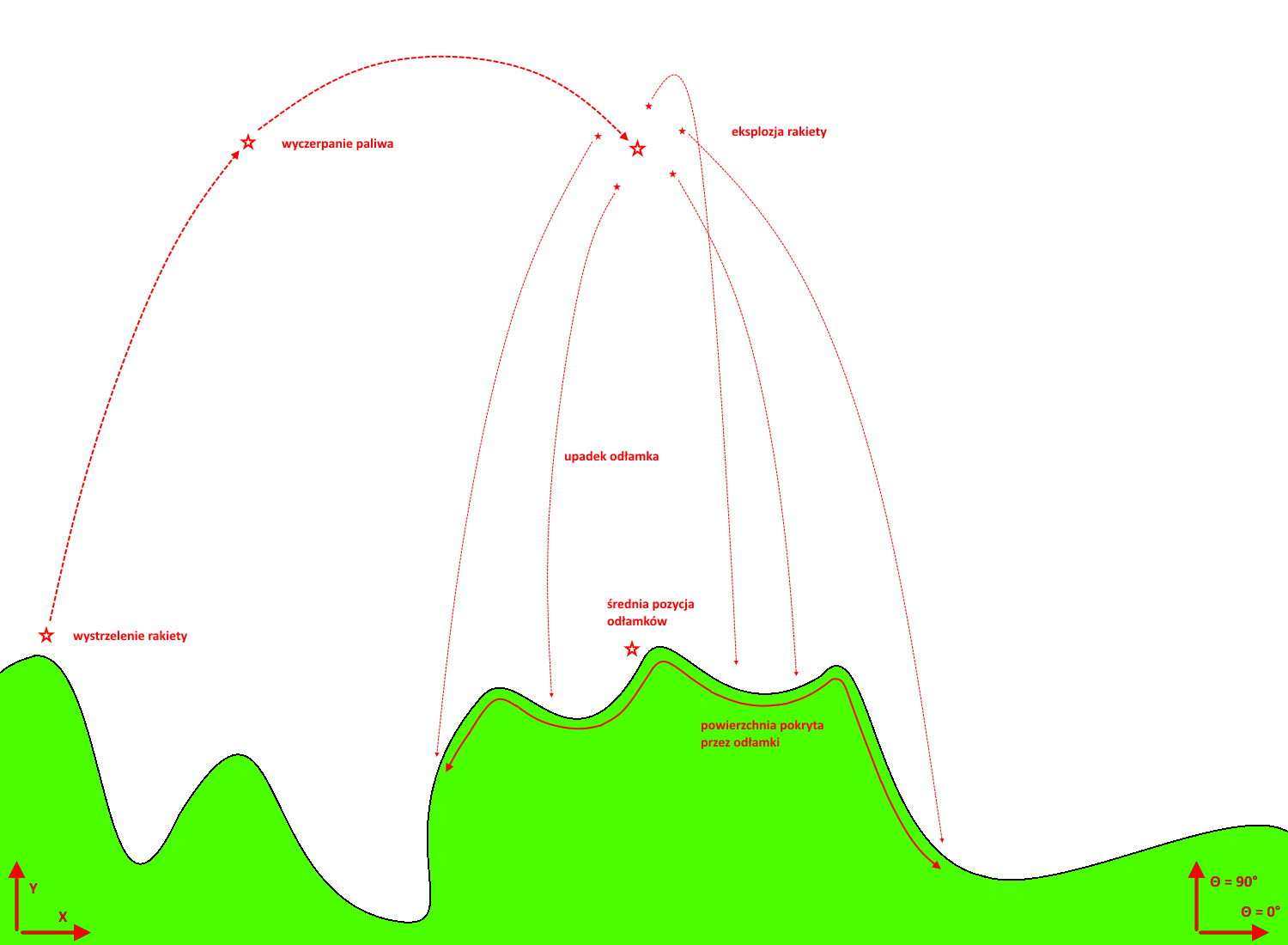
Początkowo rakieta znajduje się w stanie spoczynku w miejscu o współrzędnych (x0,y0). Rakieta zostaje odpalona w kierunku Θ w momencie t0 i do czasu wyczerpania paliwa generuje ciąg Ft w kierunku przeciwnym do Θ. Jednocześnie, w trakcie lotu rakietę spowalnia opór powietrza, wywierając siłę Fa proporcjonalną do aktualnej prędkości w kierunku przeciwnym do aktualnej prędkości. Jednocześnie oddziałuje też siła grawitacji Fg.
Początkowo masa rakiety wynosi m0, w tym m1 paliwa. Rakieta zużywa jednostkę paliwa (o masie jednostki masy) na jednostkę czasu do momentu wyczarpania paliwa.
Gdy paliwo zostanie wyczerpane, rakieta kontynuuje lot do momentu zdetonowania ładunku (wysadzenia rakiety) w momencie t2. W momencie eksplozji, rakieta zostaje ewaporowana pozostawiając za sobą 100 odłamków, równomiernie dzieląc masę rakiety pomiędzy odłamki. Eksplozja rozrzuca odłamki równomiernie we wszystkich kierunkach φ zaczynając od kierunku 0 stopnii. W chwili eksplozji odłamki zostają natychmiastowo przeniesione o jednostkę długości w kierunkach φ. Eksplozja wywiera na odłamki siłę Fe przez okres jednej jednostki czasu w kierunkach φ. Odłamki zachowują pęd rakiety, kumulując go z pędem nadawanym przez eksplozję.
Odłamki spadają do momentu upadku, wbijając się w ziemię. Odłamek przemieszczający się wiele jednostek długości w jednym kroku symulacji zatrzymuje się pod powierzchnią ziemi, w najwcześniejszym kroku symulacji w którym znajduje się pod poziomem terenu. Pozioma pozycja odłamka jest zaokrąglana do liczby całkowitej przed porównaniem z wysokością terenu.
Symulacja rozpoczyna się w zerowym czasie i trwa do momentu gdy wszystkie odłamki znajdą się w ziemi. Krok symulacji przesuwa zegar o 0.01 jednostki czasu. Obszar symulacji zajmuje 1500x1500 jednostek długości. Pozycja, prędkość i masa obiektu są aktualizowane jednocześnie. Wszystkie siły sumują się przed zastosowaniem. Czasowa długość pierwszego i drugiego etapu lotu muszą być teoretycznie dokładne.
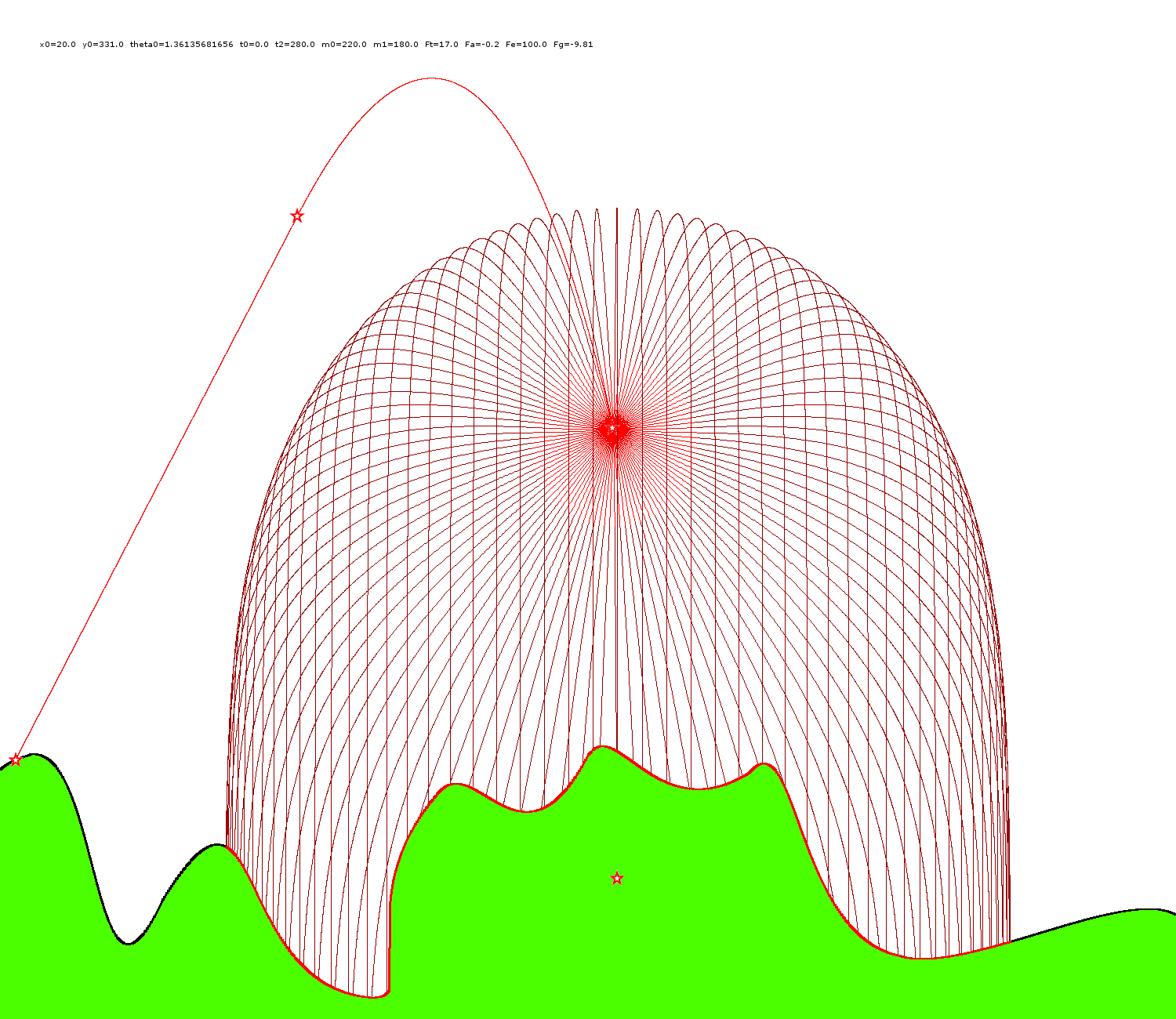
Średnia pozycja odłamków jest obliczana po zatrzymaniu się wszystkich odłamków w ziemi. Powierzchnia pokryta odłamkami jest obliczana jako długość łamanej między kolejnymi punktami terenu ograniczonymi przez najbardziej oddalone odłamki.
Format I/O
Dane wejściowe zawierają dwie linie. Pierwsza linia zawiera liczby rzeczywiste oddzielone spacjami x0, y0, theta, t0, t2, m0, m1, Ft, Fa, Fe, Fg (zdefiniowane wcześniej). Druga linia zawiera 1500 liczb całkowitych (wysokość terenu dla x=0..1499).
Dane wyjściowe zawierają pięć linii. Pierwsza linia zawiera cztery liczby px py vx vy (pozycja i prędkość rakiety w chwili wyczerpania paliwa). Druga linia zawiera cztery liczby px py vx vy (pozycja i prędkość rakiety w momencie eksplozji). Trzecia linia zawiera dwie liczby x y (średnia pozycja odłamków). Czwarta linia zawiera jedną liczbę (powierzchnia pokryta odłamkami). Piąta linia zawiera 100 liczb x (poziome pozycje odłamków w rosnącej kolejności). Wszystkie liczby są zaokrąglane do 2 miejsc po przecinku.
Przykładowe dane są dostępne do pobrania.
| Dodane przez: | Arkadiusz Bulski |
| Data dodania: | 2015-02-01 |
| Limit czasu wykonania programu: | 2s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | PYTHON PYPY PYPY3 PYTHON3 PY_NBC |
| Pochodzenie: | :) |
