| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
PYREGR - Python: Regresja |

Witajcie! Jest to drugi z serii tutoriali uczący Pythona, a w przyszłości być może nawet Cythona i Numby. Jeśli chcesz nauczyć się nowych, zaawansowanych konstrukcji to spróbuj rozwiązać kilka następnych zadań. Powodzenia!
Machine Learning to ciekawa i ostatnio popularna dziedzina zajmująca się przetwarzaniem statystycznych danych. Zastanawiałeś się w jaki sposób IMDB czy Netflix rekomendują podobne filmy? ML opiera się na fundamentalnym problemie regresji, który stanowi motyw tego zadania.
Zakładam że umiesz już posługiwać się tablicami w numpy'u. Jeśli nie, lepiej powróć do poprzednich zadań. W tym zadaniu będziesz potrzebował wielu z metod numpy'a. Wszystkie funkcje są dostępne w dokumentacji w zakładce Routines.
Zadanie
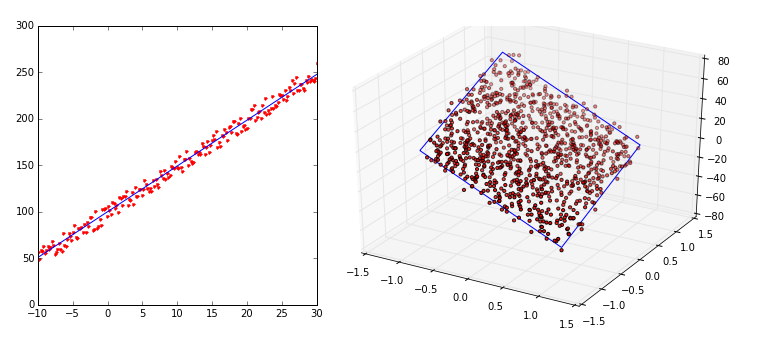
Linia trendu to funkcja liniowa, która jest jak najlepiej dopasowana do wartości w znanych punktach. Linia trendu stanowi teoretyczny model, pozwalający przewidywać wartości w nowych punktach, których faktycznie nie zmierzono. Twoim celem będzie obliczenie wartości w nieznanych jeszcze punktach, na podstawie wartości zmierzonych wcześniej.
Wymiary macierzy i wektorów dla ułatwienia wzorów:
![]()
Linia trendu to funkcja liniowa h o wpółczynnikach oznaczonych Θ oraz zmiennych oznaczonych x.
![]()
Funkcja kosztu J mierzy "jak dokładnie" linia trendu h odpowiada wartościom y zmierzonym w punktach x. Zauważ że dla każdego z m punktów, xi jest wektorem gdzie xi,1 wynosi 1.
By dopasować linię trendu do danych, będziemy potrzebować pochodnej funkcji kosztu.
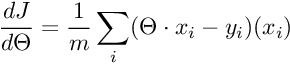
Zaczynamy od inicjalizacji współczynników Θ zerowymi wartościami. 1000 razy, równocześnie przesuwamy współczynniki proporcjonalnie (razy 0.01) do pochodnych cząstkowych funkcji kosztu względem danego współczynnika.
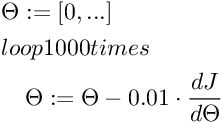
Przewidujemy wartości w nowych punktach zi używając funkcji trendu h.
![]()
Format I/O
Dane wejściowe zawierają cztery linie. Pierwsza linia zawiera liczby m (ilość znanych punktów) n (ilość zmiennych) q (ilość zapytań). Druga linia zawiera liczby x (argumenty znanych wartości, skonkatenowane kolejne wektory). Trzecia linia zawiera liczby y (znane wartości). Czwarta linia zawiera liczby z (argumenty zapytań, skonkatenowane kolejne wektory).
Dane wyjściowe zawierają jedną linię. Linia zawiera q liczb zaokrąglonych do 2 miejsc po przecinku.
Przykładowe dane można pobrać tutaj.
| Dodane przez: | Arkadiusz Bulski |
| Data dodania: | 2015-01-21 |
| Limit czasu wykonania programu: | 1s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | PYTHON PYPY PYTHON3 |
| Pochodzenie: | :) |
