| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
PYNE - Python: Strategie |

Witajcie! Jest to kolejny z serii tutoriali uczący Pythona, a w przyszłości być może nawet Cythona i Numby. Jeśli chcesz nauczyć się nowych, zaawansowanych konstrukcji to spróbuj rozwiązać kilka następnych zadań. Powodzenia!
Teoria gier pozwala przewidywać wyniki gier, gdzie każdy gracz, starając się zyskać samemu jak najwięcej, podejmuje decyzje bez negocjacji z innymi graczami.
Zadanie
Mamy dwóch graczy, jeden gracz wybiera jeden z wierszy jako swoją strategię (swój ruch), drugi gracz wybiera jedną z kolumn jako swoją strategię. Profil strategii (kombinacja wiersza i kolumny) wyznacza zysk każdego z graczy, najpierw zysk gracza wierszowego, potem zysk gracza kolumnowego.
Okazuje się że jeden z wyników gry jest "pewny". Wynika to z prostego faktu: gracze nigdy nie wybierają strategii jeśli inna strategia zawsze będzie bardziej korzystna, bez względu na strategię przeciwnika. Jeśli usuniemy wszystkie silnie zdominowane strategie z gry poniżej, zostanie tylko jeden możliwy (racjonalny) wynik gry, nazywany equilibrium Nasha.
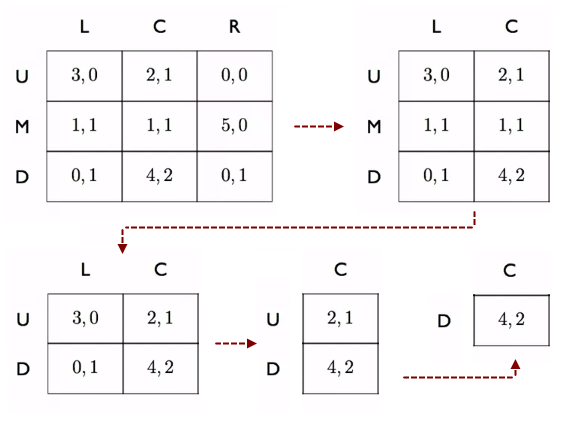
By znaleźć ostateczny profil strategii, będziemy wielokrotnie szukać i usuwać strategie, których zysk dla swojego gracza jest niższy (<) niż wybrana inna strategia tego samego gracza. Nie ma znaczenia w jakiej kolejności strategie będą usuwane, ale dopiero usunięcie jednej strategii może ujawnić inne strategie. Także po usunięciu każdej strategii trzeba szukać od nowa. Ważne jest to że wektor reprezentujący zysk z dominowanej strategii musi być zdecydowanie mniejszy, nierówny, od wektora strategii dominującej.
Dla przykładu powyżej, gracz kolumnowy może skreslić strategię R, strategia R daje mu możliwe zyski [0 0 1] podczas gdy strategia C da zysk [1 1 2], dając większy zysk w odpowiedzi dla każdego ruchu przeciwnika. Dlatego kolumna R została usunięta. Następnie gracz wierszowy usuwa wektor M, gdyż zyski [1 1] są zawsze niższe niż [3 2]. Następnie zysk [0 1] jest niższy niż [1 2]. Na końcu zysk 2 jest niższy niż 4.
Profil strategii który zostaje na końcu procesu stanowi rozwiązanie problemu. Interesuje nas numer wiersza i kolumny ostatecznych strategii oraz zyski graczy.
Format I/O
Dane wejściowe stanowią linie. Pierwsza linia zawiera liczby m (wysokość tablicy) n (szerokość tablicy). Kolejne linie zawierają po jednym z wierszu tablicy, pary liczb całkowitych oddzielonych przecinkami, komórki oddzielone spacjami.
Dane wyjściowe stanowi jedna linia. Zawiera liczby całkowite: indeks strategii wiersza, indeks strategii kolumny, zysk gracza wierszowego, zysk gracza kolumnowego.
Dane przykładowe są dostępne do pobrania.
| Dodane przez: | Arkadiusz Bulski |
| Data dodania: | 2015-01-30 |
| Limit czasu wykonania programu: | 2s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | PYTHON PYPY PYPY3 PYTHON3 PY_NBC |
| Pochodzenie: | :) |
