| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
MANDEL - Fraktaliusz i Algorytmus: Żuk |
Czy kiedykolwiek miałeś to uczucie, że nie byłeś pewien czy to jawa czy wciąż sen?
Neo, Matrix 1999
Z całą pewnością tego uczucia doznał Fraktaliusz, który trafił do świata różniącego się od tego, który zna na codzień. Znajdował się on na polanie, przez środek której biegł rozległy trakt, a na nim, w oddali, widać było zbliżającą się postać... Był to mężczyzna odziany w długi płaszcz, spiczasty kapelusz i drewnane sandały, a wokół siebie roztaczał aurę podejrzliwości. Postać zbliżyła się do naszego bohatera i spojrzała w jego kierunku:
- Witaj. Już myślałem, ze zostanę tu na wieki! - rzekł mężczyzna.
- Kim jesteś? I co to za miejsce? - odrzekł Fraktaliusz.
- Jestem Algorytmus i czekałem na kogoś, kto pomoże mi się stąd wydostać. Widzisz, dzięki temu berłu mogę tworzyć realne obiekty z obiektów matematycznych. Niestety przebywam tu już tak długo, że zapomniałem wszystkie równania... Potrzebuje więc kogoś kto będzie w stanie to zrobić za mnie.
- Bierzmy się zatem do pracy. Czego potrzebujesz?
- Na początek Żuka... Tak... Żuk Mandelbrota nada się w sam raz.
Pomoż naszym bohaterom wydostać się z tej przedziwnej krainy i wygeneneruj Żuka Mandelbrota, który będzie mógł zostać stworzony przez Algorytmusa.
Płaszczyzna, na której generowany jest zbiór, jest podzbiorem płaszczyzny zespolonej, której zakresy wartości określone za pomocą przedziałów domkniętych, odpowiednio:
- [-2.0, 1.0] dla osi OX
- [-1.0, 1.0] dla osi OY
kolejne znaki wyjścia reprezentują kolejne punkty tego obszaru po przeskalowaniu w taki sposób, aby obszar ten miał szerokość x oraz wysokość y. Oś OX odpowiada wartości części rzeczywisej liczby p, a oś OY jej części urojonej.
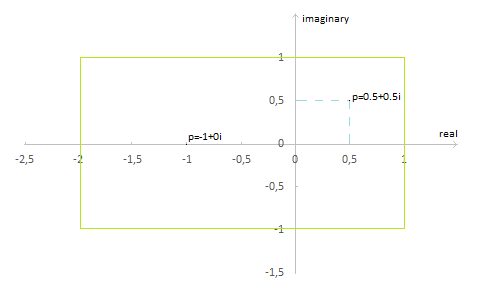
Część płaszczyzny prezentowana na wyjściu, z przykładowymi punktami p.
Zbiór Mandelbrota tworzą punkty p należące do zbioru liczb zespolonych, dla których ciąg określony równaniem rekurencyjnym:
![]()
przykładowo dla punktu (0.3, 0.6):
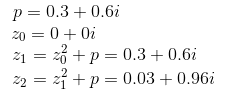
nie dąży do nieskończoności. Jest to jednoznaczne z tym, że moduł żadego z wyrazów ciągu nie przekracza 2:
![]()
Można zauważyć, że zarówno ciąg, jak i kolejne wartości modułów jego elementów, po osiągnięciu wartości |zn|>=2 są monotoniczne i bardzo szybko rosną do nieskończoności.
Aby znaleźć zbiór wynikowy oblicza się m początkowych wyrazów ciągu dla każdego punktu p na płaszczyźnie, na której będziemy reprezentować nasz wynik. Wypisywany symbol zależy od stosunku ilości początkowych wyrazów ciągu (nie uwzględniając z0), których moduł jest mniejszy niż 2 do m:
- 100%: O
- ponad 75.0 %: o
- ponad 50.0 %: ;
- ponad 25.0 %: ,
- mniej lub równo 25.0 %: .
Wejście
W pierwszej lini wejścia zajdują się 3 liczby: x, y, t (20 < x, y < 300; 0 < t < 300) oznaczające odpowiednio szerokość generowanego obrazu, jego wysokość oraz liczbę testów.
W kolejnych t liniach jedna liczba m (0 < m < 66) oznaczająca liczbę itereacji.
Wyjście
Dla każdego testu x linii po y znaków: zbiór Mandelbrota wygenerowany zgodnie z opisem w zadaniu.
Po każdym teście dodatkowa pusta linia.
Przykład
Wejście:99 39 199 39 1 20
Wyjście: ...........................................................,,o,,,,................................. ..........................................................,,,,O;,,................................. ........................................................,,,,OoOo,,,................................ .......................................................,OoooOOOO;;;,............................... .....................................................,,,,;OOOOOOOO,,,.............................. ...................................................,,,,,,;OOOOOOOO,,,,............................. .............................................;,,o,,,,,,,;;oOOOOOO;;,,,;,,,,,,;,.................... ............................................,,OOOo;,;OOOOOOOOOOOOOOOoOO;,,,,,;,,................... ...........................................,,,,oOOOOOOOOOOOOOOOOOOOOOOOO;OOOOOO,................... ...........................................,,,,;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,.................... .........................................,,;OooOOOOOOOOOOOOOOOOOOOOOOOOOOOOo;,,,................... .......................,,,..........,,,,,,,;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,,,.................. .......................,;,,,,,,,O,,,,,,,,,;oOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoO;;,................. .......................,,OO;o,,;oO,;,,,,,,;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO;,.................. ......................,,,,;OOOoOOOOOoO,,,;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,,.................. ....................,,,,,,;OOOOOOOOOOOO;;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,.................. ...................,,,,,;OOOOOOOOOOOOOOOoOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,,.................. ................,,,,o;o;;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOo,................... .......,,,,..,,,,,,;oOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,,.................... .OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO;,,,.................... .......,,,,..,,,,,,;oOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,,.................... ................,,,,o;o;;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOo,................... ...................,,,,,;OOOOOOOOOOOOOOOoOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,,.................. ....................,,,,,,;OOOOOOOOOOOO;;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,.................. ......................,,,,;OOOoOOOOOoO,,,;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,,.................. .......................,,OO;o,,;oO,;,,,,,,;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO;,.................. .......................,;,,,,,,,O,,,,,,,,,;oOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoO;;,................. .......................,,,..........,,,,,,,;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,,,.................. .........................................,,;OooOOOOOOOOOOOOOOOOOOOOOOOOOOOOo;,,,................... ...........................................,,,,;OOOOOOOOOOOOOOOOOOOOOOOOOOOOOO,.................... ...........................................,,,,oOOOOOOOOOOOOOOOOOOOOOOOO;OOOOOO,................... ............................................,,OOOo;,;OOOOOOOOOOOOOOOoOO;,,,,,;,,................... .............................................;,,o,,,,,,,;;oOOOOOO;;,,,;,,,,,,;,.................... ...................................................,,,,,,;OOOOOOOO,,,,............................. .....................................................,,,,;OOOOOOOO,,,.............................. .......................................................,OoooOOOO;;;,............................... ........................................................,,,,OoOo,,,................................ ..........................................................,,,,O;,,................................. ...........................................................,,o,,,,.................................
Wejście:
30 20 2
4
8
Wyjście: .....,,,,,,,,;;;OOOO;;;,,..... ....,,,,,,,,;;;OOOOOO;;,,,.... ...,,,,,,,,;;;OOOOOOOOO;,,,... ...,,,,,,;;;OOOOOOOOOOOO;,,... ..,,,,,,;;OOOOOOOOOOOOOOO,,,.. .,,,,,;OOOOOOOOOOOOOOOOOO;,,,. .,,,;;OOOOOOOOOOOOOOOOOOO;,,,. .,;;;OOOOOOOOOOOOOOOOOOOO;,,,. .;;;OOOOOOOOOOOOOOOOOOOOO;,,,. .OOOOOOOOOOOOOOOOOOOOOOOO;,,,. .OOOOOOOOOOOOOOOOOOOOOOOO;,,,. .;;;OOOOOOOOOOOOOOOOOOOOO;,,,. .,;;;OOOOOOOOOOOOOOOOOOOO;,,,. .,,,;;OOOOOOOOOOOOOOOOOOO;,,,. .,,,,,;OOOOOOOOOOOOOOOOOO;,,,. ..,,,,,,;;OOOOOOOOOOOOOOO,,,.. ...,,,,,,;;;OOOOOOOOOOOO;,,... ...,,,,,,,,;;;OOOOOOOOO;,,,... ....,,,,,,,,;;;OOOOOO;;,,,.... .....,,,,,,,,;;;OOOO;;;,,..... .............,,,,;OO,,,....... ............,,,,,OOO,,,....... ...........,,,,;;OOO;,,,...... .........,,,,;OoOOOOOo;O,..... ........,,,,;;OOOOOOOOOO,..... ......,,,,,;;OOOOOOOOOOo,,.... ....,,,Oooo;oOOOOOOOOOOO;,.... ..,,,,;oOOOOOOOOOOOOOOOO;,.... .,,,,;oOOOOOOOOOOOOOOOOO,,.... .,;;;OOOOOOOOOOOOOOOOOOo,,.... .,;;;OOOOOOOOOOOOOOOOOOo,,.... .,,,,;oOOOOOOOOOOOOOOOOO,,.... ..,,,,;oOOOOOOOOOOOOOOOO;,.... ....,,,Oooo;oOOOOOOOOOOO;,.... ......,,,,,;;OOOOOOOOOOo,,.... ........,,,,;;OOOOOOOOOO,..... .........,,,,;OoOOOOOo;O,..... ...........,,,,;;OOO;,,,...... ............,,,,,OOO,,,....... .............,,,,;OO,,,.......
| Dodane przez: | Jaroslaw Konczak |
| Data dodania: | 2018-06-10 |
| Limit czasu wykonania programu: | 1s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: GOSU |
