| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
FR_05_18 - Curling v2! |
Curling v2
Pewnego dnia Jasiowi bardzo się nudziło i postanowił pooglądać TV. Po żmudnej wędrówce po kanałach napotkał transmisję zawodów gry w Curling. Jasiu zaciekawiony nowo poznaną dyscypliną sportową postanowił zagrać ze znajomymi w grę o podobnych zasadach.
Zasady gry:
- W grze biorą udział dwie drużyny.
- Każda drużyna ma do dyspozycji tyle samo kamieni.
- Grę zawsze zaczyna drużyna czerwona.
- Ruchy odbywają się na przemian.
- Rozgrywana będzie zawsze dokładnie jedna runda, która kończy się wraz z wyrzuconym ostatnim kamieniem drużyny żółtej.
- Drużyna przed wykonanym rzutem ma wybór z którego miejsca (p) o współrzędnych (p,-11), gdzie (-2<=p<=2),
będzie rzucać swój kamień.
- Wyrzucony kamień z miejsca p może trafić w sektor osi OX z przedziału [5*p-5,5*p+5]
- Przed rzutem drużyna podaje w które miejsce chce oddać swój rzut.
- W przypadku, gdy cel nie zawiera się w możliwym sektorze drużyna traci swój rzut.
- Zakłada się, że przynajmniej jeden kamień trafi w dom, który jest kołem o równaniu x^2+y^2=100.
- Zwycięża ta drużyna, która umieści swój kamień bliżej środka koła.
- W przypadku remisu żadna z drużyn nie jest zwycięzcą.
- W przypadku gdy wyrzucony kamień na swojej drodze do celu napotyka inny kamień dochodzi do zderzenia.
- Podczas zderzenia kamień uderzający zatrzymuje się na pozycji uderzanego. Natomiast uderzany przeskakuje w zależności od miejsca (p) uderzającego zawsze o 1 jednostkę na osi OY do przodu oraz o +|p| jednostek na OX, jeśli współrzędna x osiągnięta w momencie zderzenia jest większa od miejsca wyrzutu lub o -|p| w zdarzeniu przeciwnym.
- Zakłada się, że występują tylko zderzenia centralne, a każde uderzenie z p równego 0 jest poprawnie rozpatrzone według powyższych reguł.
- W przypadku napotkania innego kamienia przez uderzony już wcześniej kamień stosuje się przeskok analogiczny do wyżej opisanych reguł za wyjątkiem (p), które zawsze pochodzi od rzutu wywołującego ciąg zderzeń.
Wejście:
W pierwszym wierszu znajduje się mała liczba nieparzysta k oznaczająca ilość wyrzuconych kamieni .
W kolejnych k wierszach znajdują się 3 liczby x,y,p. Pierwsza i druga oznacza współrzędne celu kamienia podane przez drużynę i miejsce p, z którego został kamień wyrzucony. |X|<16,(-10<=Y<=16).
W kolejnym wierszu znajduje się liczba t określająca liczbę zapytań. (1<=t<=10^6)
W następnych t wierszach znajdują się 3 liczby x,y,p oznaczające pierwszą i drugą współrzędną będącą celem ostatniego kamienia drużyny żółtej i miejsce, z którego drużyna rzuca swój ostatni kamień.
Wyjście:
Odpowiedź „TAK”, jeżeli wygra drużyna żółta, w przeciwnym wypadku „NIE”. Dodatkowo, jeśli „TAK”, należy podać ilość punktów w nawiasie kwadratowym, które definiowane są jako 1 punkt za każdy kamień zwycięskiej drużyny leżący bliżej od najbliżej położonego względem środka koła kamienia drużyny przeciwnej.
Przykład:
Wejście: 5 -2 0 0 -1 0 -1 0 -7 1 -1 -3 1 -1 -3 1 3 0 0 0 0 0 1 0 0 2
Wyjście: TAK [1] TAK [2] TAK [1]
Wytłumaczenie przeskoków dla kamyka na (-5.0):
a) Uderzonego przez inny kamyk z p=0. (-5.0)->(-5.1)
b) Uderzonego przez inny kamyk z p=-2. (-5.0)->(-7.1)
c) Uderzonego przez inny kamyk z p=1. Rzut niemożliwy
Wytłumaczenie przykładu:
Sytuacja przed zapytaniami:
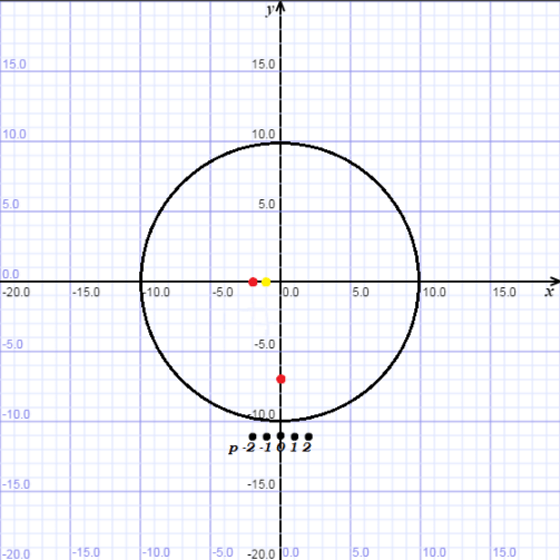
Sytuacja po zapytaniu pierwszym:
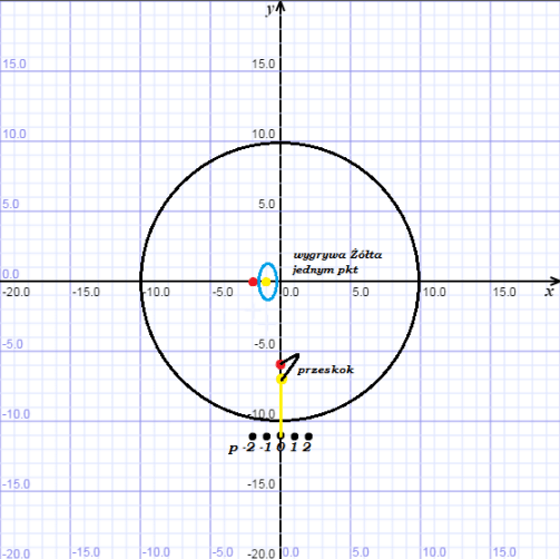
Sytuacja po zapytaniu drugim:
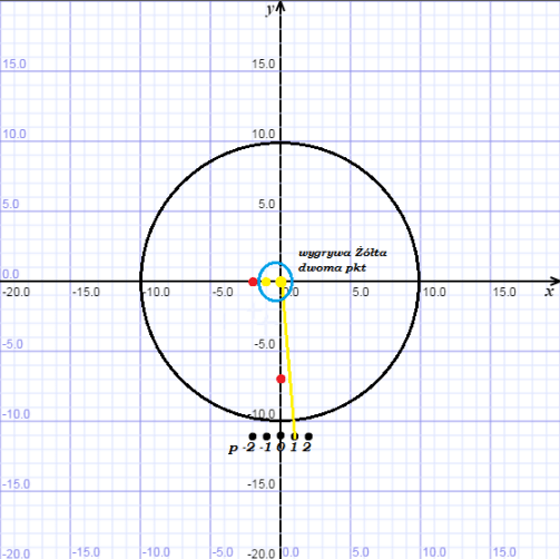

| Dodane przez: | Szymon Witkowski |
| Data dodania: | 2016-03-02 |
| Limit czasu wykonania programu: | 1s-2s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: GOSU |
