| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
ETI07E4 - Spadająca kulka |
W pewnej grze komputerowej akcja toczy się na prostokątnej planszy złożonej z kwadratowych pól o rozmiarze jednostkowym. Wyróżnia się tylko pola całkowicie puste i całkowicie pełne.
Na potrzeby symulacji w świecie tym zdefiniowano dosyć specyficzne prawa fizyki. Przypuśćmy, że w pewnym pustym polu zostanie umieszczona i puszczona swobodnie mała kuleczka. Wówczas na początku każdej jednostki czasu znajduje się ona zawsze w całości w pewnym pustym polu. W ciągu jednostki czasu kulka wykonuje ruch zgodnie z następującymi zasadami:
- Kulka znajdująca się na pustym polu, pod którym nie ma pola pełnego, wykonuje zawsze ruch o jedno pole w dół.
- Kulka znajdująca się na pustym polu, pod którym jest pole pełne, wykonuje z równym prawdopodobieństwem ruch albo o jedno pole w lewo, albo o jedno pole w prawo. Wybrany ruch nie zostaje jednak wykonany, jeżeli pole docelowe jest pełne.
Kulka, przemieszczając się, może wypaść poza planszę (wszystkie pola wokół planszy należy traktować jako puste).
Znając używaną w grze planszę oraz położenie początkowe kulki, należy wyznaczyć prawdopodobieństwo, że tor kulki przejdzie przez wskazane puste pola.
Wejście
Wejście rozpoczyna się od dwóch liczb całkowitych y x oddzielonych spacją, określających wymiary planszy (1 <= x, y <=100). W każdym z kolejnych y wierszy znajduje się opis rzędów planszy (poczynając od góry), złożony z dokładnie x znaków, określających zapełnienie poszczególnych pól rzędu. Pole zajęte zapisane jest zawsze w postaci znaku 'x', a pole puste jako jeden ze znaków {'*', '1', '2', '3', '.'}. Każdy ze znaków {'*', '1', '2', '3'} pojawia się dokładnie raz w całej planszy, a znak '*' opisuje położenie początkowe kulki.
Można przyjąć, że w jednym rzędzie planszy pola pełne nigdy do siebie bezpośrednio nie przylegają.
Wyjście
Wyjście składa się z dokładnie trzech wierszy, w których należy kolejno podać prawdopodobieństwa przejścia kulki przez puste pola oznaczone '1', '2', '3'. Wartość prawdopodobieństw powinna być określona dokładnie (bez zaokrąglenia czy obcięcia) w postaci ułamka dziesiętnego. Należy zawsze wybrać najkrótszy poprawny zapis ułamka.
Przykłady
Zestaw przykładowy 1 Wejście: 9 7 ....... ...*... ....... ...x... ....... ..x.x.. ....... .1.2.3. ....... Wyjście: 0.25 0.5 0.25
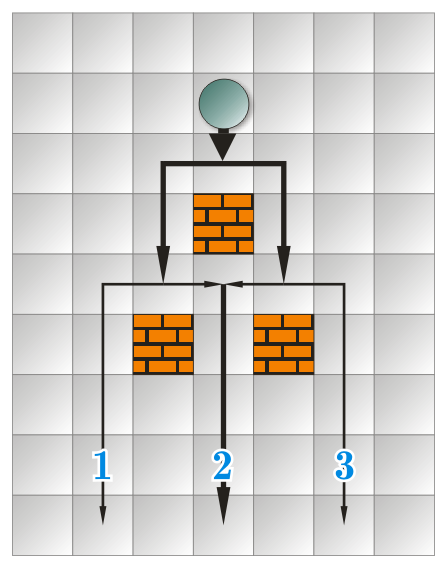
Ilustracja przykładu 1
Zestaw przykładowy 2 Wejście: 5 5 ..*.3 ..x.. .x.x2 ..... x1... Wyjście: 0.25 0.5 0
| Dodane przez: | adrian |
| Data dodania: | 2006-11-11 |
| Limit czasu wykonania programu: | 1s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: GOSU |
