| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
ETI06F1 - Pole pewnego koła |
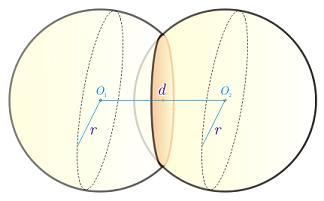
Wyznacz pole koła, którego okrąg jest przecięciem dwóch identycznych sfer o promieniu r. Odległość pomiędzy środkami sfer wynosi d. Wartości r oraz d podane na wejściu są liczbami zmiennoprzecinkowymi. Można założyć, że 1 <= d < 2 * r <= 2000.
Wejście
Na wejściu podane są dwie liczby zmiennoprzecinkowe r d oddzielone spacją, oznaczające odpowiednio promień sfery i odległość między środkami sfer.
Wyjście
Należy wypisać pojedynczą liczbę zmiennoprzecinkową S oznaczającą pole koła. Dopuszczalny błąd wyniku wynosi 0.01.
Uwaga. W roli separatora dziesiętnego należy używać kropki (nie: przecinka). Można przyjąć, że stosunek obwodu koła do jego średnicy wynosi 3.141592654.
Liczba punktów za zadanie jest równa liczbie poprawnie rozwiązanych testów / 5. Testów jest 20.
Przykład
Przykład 1 Wejście: 10 10 Wyjście: 235.62 Przykład 2 Wejście: 1000 1500 Wyjście: 1374446.79
| Dodane przez: | mima |
| Data dodania: | 2005-11-11 |
| Limit czasu wykonania programu: | 1s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: GOSU |
