| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
BALANCE - Waga Szalkowa |
Doktor Farmaceutyk zapisał cioci Kloci mnóstwo lekarstw na wszelkie przypadłości. Każde lekarstwo ciocia Klocia musi dokładnie zważyć przed zażyciem. Posługuje się w tym celu wagą szalkową i odważnikami o dwóch nominałach (czyli wagach). Na przykład, zakładając, że ciocia ma odważniki o wadze 300 mg i 700 mg, może zważyć 200 mg aspiryny na dwa sposoby.
Sposób 1: na jednej szalce kładzie trzy odważniki 300-miligramowe, a na drugiej jeden odważnik 700-miligramowy oraz taką dawkę aspiryny, aby waga zrównoważyła się, tzn. łączny ciężar na obu szalkach był taki sam.
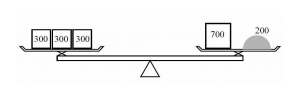
Sposób 2: na jednej szalce kładzie dwa odważniki 700-miligramowe, a na drugiej cztery odważniki 300-miligramowe oraz taką dawkę leku, aby waga była w równowadze.
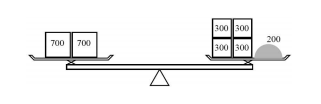
Oczywiście drugi sposób jest dla cioci bardziej uciążliwy, gdyż wymaga użycia większej liczby odważników, które na dodatek więcej w sumie ważą.
Napisz program, który pomógłby cioci Kloci wygodnie ważyć lekarstwa.
Wejście
Wejście zawiera nieokreśloną liczbę (≤ 104) zestawów danych. Każdy zestaw jest podany w jednym wierszu i składa się z trzech liczb całkowitych a, b i d (a ≠ b, 1 ≤ a, b ≤ 50 000, 0 ≤ d ≤ 50 000) oddzielonych pojedynczym odstępem. Liczby a i b oznaczają wagi odważników (w miligramach), którymi dysponuje ciocia Klocia. Liczba d oznacza wagę (w miligramach) lekarstw, którą należy zmierzyć. Zakładmy, że ciocia dysponuje dowolną liczbą odważników o masie a mg i o masie b mg. Wejście jest zakończone wierszem zawierającym trzy zera.
Wyjście
Dla każdego zestawu danych należy wypisać w osobnym wierszu słowo BRAK, jeśli niemożliwe jest zważenie d mg lekarstw za pomocą dowolnej liczby odważników o masie a mg i b mg. W przeciwnym wypadku należy wypisać dwie nieujemne liczby całkowite x i y (oddzielone pojedynczym odstępem), takie że:
- d mg lekarstwa można odmierzyć używając dokładnie x odważników o masie a mg oraz y odważników o masie b mg
- x+y to minimalna liczba odważników o wadze a mg i b mg pozwalająca odmierzyć d mg lekarstwa
- wśród zestawów x+y odważników o wadze a mg i b mg pozwalających odmierzyć d mg lekarstwa, zestaw x odważników o masie a i y o masie b ma najmniejszą sumaryczną masę
Przykład
Wejście:
700 300 200
500 200 300
500 200 500
275 110 330
275 110 385
648 375 4002
3 1 10000
0 0 0
Wyjście:
1 3
1 1
1 0
0 3
1 1
49 74
3333 1
| Dodane przez: | Rafal Nowak |
| Data dodania: | 2005-03-26 |
| Limit czasu wykonania programu: | 1s |
| Limit długości kodu źródłowego | 5000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: GOSU |
| Pochodzenie: | Wiosenny konkurs dla przyszłych studentów Instytutu Informatyki Uniwersytetu Wrocławskiego |
