| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_27_04 - Najcenniejsza ścieżka |
Bajtek na ostatnie urodziny dostał w prezencie zestaw do gry w szachy heksagonalne. Jednak ponieważ bardzo szybko osiągnął poziom arcymistrzowski, zwykła gra nudzi go już. Chłopiec postanowił więc, że planszę i figurę białego króla wykorzysta do opracowania pewnej łamigłówki. Oto jej zasady.
Przypisujemy każdemu polu pewną wartość punktową. Następnie stawiamy króla na dowolnym polu w pierwszej kolumnie i dozwolonymi dla niego ruchami staramy przedostać się na dowolne pole w ostatniej kolumnie, tak aby uzyskać największą możliwą sumę wartości odwiedzonych pól. Jedyne ograniczenie jest takie, że w każdym ruchu król musi zostać przesunięty na pole w kolumnie o wyższym numerze.
Poniższy rysunek przedstawia klasyczną planszę do szachów heksagonanych oraz króla w jednej z dozwolonych pozycji wyjściowych i pola możliwe do osiągnięcia w pierwszym ruchu.
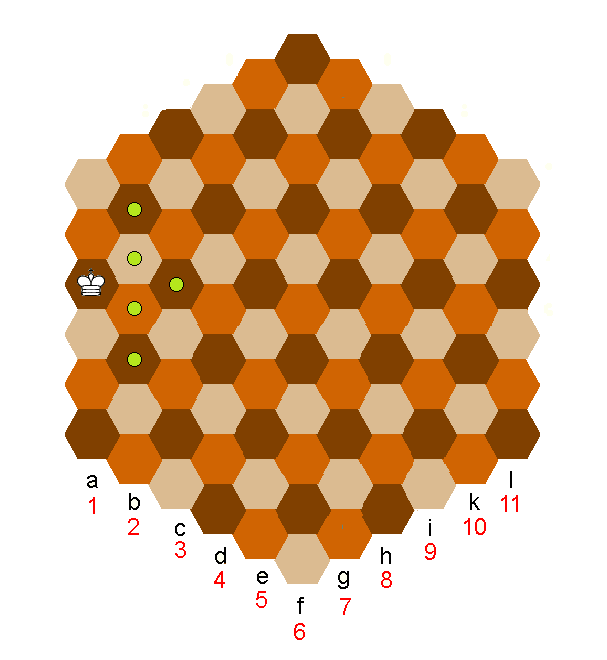
Bajtek planuje opracować wiele plansz o różnych rozmiarach i z różnymi wartościami poszczególnych pól. Jako rozmiar planszy przyjmujemy liczbę pól na dowolnym boku (plansza na rysunku ma rozmiar 6). Twoim zadaniem jest napisać program, który wyznaczy maksymalną możliwą do uzyskania na danej planszy sumę.
Wejście
W pierwszym wierszu liczba plansz t (t ≤ 100).
Dla każdej planszy w jednej linii jej rozmiar n (2 ≤ n ≤ 100), a w następnej linii odpowiednia ilość liczb całkowitych wi oznaczających wartości punktowe wszystkich pól na planszy (-109 ≤ wi ≤ 109). Liczby podane są kolumnami od lewej do prawej, a w każdej kolumnie od dołu do góry.
Wyjście
Dla każdej planszy, w osobnej linii maksymalna możliwa do uzyskania suma wartości pól odwiedzonych przez króla.
Przykład
Wejście: 2
2
1 5 3 -2 1 -3 -1
3
5 -1 -2 -3 -3 -6 0 -20 -20 -20 -20 -20 -10 -10 -10 0 3 1 -1 Wyjście:
7
0
Pomoc do przykładu:
Poniższy rysunek przedstawia pierwszą planszę z przykładu.
| Dodane przez: | Witold Długosz |
| Data dodania: | 2016-04-25 |
| Limit czasu wykonania programu: | 1s-2s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ASM64 GOSU JS-MONKEY |

