| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_14_09 - Wybitność szczytu |
 Wybitność szczytu to, mówiąc kolokwialnie, miara tego, na ile się on wyróżnia spośród swego otoczenia. Bardziej precyzyjnie jest to najmniejszy możliwy spadek wysokości, który musi wystąpić na ścieżce z tego szczytu do pewnego punktu położonego wyżej niż ten szczyt. Mamy daną cyfrową mapę terenu rozmiaru n na m. Każdy punkt (piksel) na tej mapie odpowiada pewnej całkowitej wysokości nad poziomem morza. Twoim zadaniem jest określenie wybitności zadanych punktów w terenie. Dwa punkty na mapie sąsiadują ze sobą jeżeli stykają się jednym z boków lub jednym z rogów – stąd każdy punkt może mieć co najwyżej ośmiu sąsiadów. Poprawną ścieżką w terenie jest więc dowolny ciąg punktów (p1, p2, p3, ... , pk), w którym kolejne pary punktów (p1, p2), (p2, p3), (p3, p4) ... (pk-1, pk) sąsiadują ze sobą na mapie.
Wybitność szczytu to, mówiąc kolokwialnie, miara tego, na ile się on wyróżnia spośród swego otoczenia. Bardziej precyzyjnie jest to najmniejszy możliwy spadek wysokości, który musi wystąpić na ścieżce z tego szczytu do pewnego punktu położonego wyżej niż ten szczyt. Mamy daną cyfrową mapę terenu rozmiaru n na m. Każdy punkt (piksel) na tej mapie odpowiada pewnej całkowitej wysokości nad poziomem morza. Twoim zadaniem jest określenie wybitności zadanych punktów w terenie. Dwa punkty na mapie sąsiadują ze sobą jeżeli stykają się jednym z boków lub jednym z rogów – stąd każdy punkt może mieć co najwyżej ośmiu sąsiadów. Poprawną ścieżką w terenie jest więc dowolny ciąg punktów (p1, p2, p3, ... , pk), w którym kolejne pary punktów (p1, p2), (p2, p3), (p3, p4) ... (pk-1, pk) sąsiadują ze sobą na mapie.
Wejście
W pierwszej linii wejścia podane są trzy, oddzielone spacjami liczby całkowite n, m oraz k (2<=n, m<=1000, 1<=k<=100) oznaczające odpowiednio wysokość i szerokość mapy oraz liczbę zapytań. W kolejnych n wierszach wejścia podane jest po m liczb całkowitych (z zakresu od 0 do 8848) odpowiadających wysokościom kolejnych punktów na mapie. W kolejnych k wierszach podane są po dwie oddzielone spacjami liczby całkowite ai oraz bi (1<=ai<=n, 1<=bi<=m) oznaczające współrzędne punktów, których wybitność należy policzyć.
Wyjście
Dla każdego zapytania w oddzielnej linii należy podać liczbę całkowitą oznaczającą wybitność podanego punktu. Zakładamy, że jeżeli nie istnieje punkt wyższy od danego punktu, to jego wybitność równa się jego wysokości nad poziomem morza.
Przykład
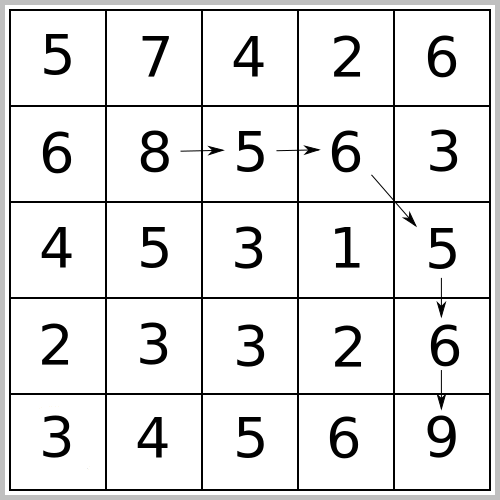
Wejście: 5 5 3 5 7 4 2 6 6 8 5 6 3 4 5 3 1 5 2 3 3 2 6 3 4 5 6 9 2 2 2 4 5 5 Wyjście: 3 1 9
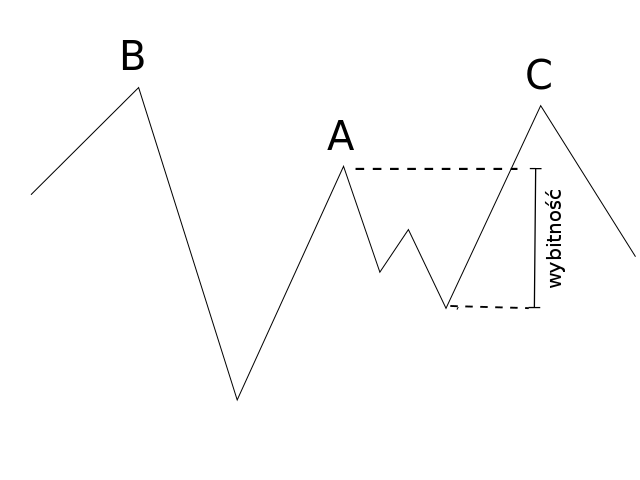
Rysunek do przykładu: Ilustracja wybitności szczytu A:
Aby z punktu (2, 2) o wysokości 8 metrów dostać się do terenu
wyżej położonego (ten warunek spełnia tylko punkt (5, 5)) możemy wybrać ścieżkę, która obniża się tylko o 3 metry
(najniższy punkt na ścieżce ma wysokość 5 metrów).
| Dodane przez: | Ostry |
| Data dodania: | 2014-02-09 |
| Limit czasu wykonania programu: | 1s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ASM64 GOSU |