| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_11_10 - Jak Bajtek mechanizmy wielce złożone konstruował |
 W całej Bajtocji wszem wiadomo, iż Bajtek, syn królewski, dzieckiem wielce uzdolnionym jest i talenty swe wszelakie wciąż rozwija. Inaczej być nie może, skoro pragnieniem ojca jego - Bajtolomeusza jest, aby syn w każdej nauki dziedzinie mistrzem został. Król o edukacyję potomka swego dba więc wyśmienicie. Dopiero co Bajtek z różnorodnymi systemami zapisywania liczb zaznajomiony został (w szczególności system oktalny chłopiec sobie upodobał), a już czas nadszedł, aby w dziedzinie konstrukcji machin wszelakich w przekładnie wyposażonych, najwyższy poziom wiedzy i umiejętności osiągnął.
W całej Bajtocji wszem wiadomo, iż Bajtek, syn królewski, dzieckiem wielce uzdolnionym jest i talenty swe wszelakie wciąż rozwija. Inaczej być nie może, skoro pragnieniem ojca jego - Bajtolomeusza jest, aby syn w każdej nauki dziedzinie mistrzem został. Król o edukacyję potomka swego dba więc wyśmienicie. Dopiero co Bajtek z różnorodnymi systemami zapisywania liczb zaznajomiony został (w szczególności system oktalny chłopiec sobie upodobał), a już czas nadszedł, aby w dziedzinie konstrukcji machin wszelakich w przekładnie wyposażonych, najwyższy poziom wiedzy i umiejętności osiągnął.
Bajtek, pokaźny zbiór barwnych kół zębatych i łańcuchów różnej długości (do łączenia tych pierwszych przeznaczonych) od ojca swego niedawno otrzymał, a zabawa, która na konstruowaniu z tychże elementów przekładni różnorakich polega, bardzo go teraz zajmuje. Chłopiec, systemy coraz bardziej złożone budować potrafi, w których to mnóstwo kółek połączonych jest parami bez pośrednictwa żadnego (to przekładnia zębata) lub z użyciem łańcucha (to zaś przekładnia łańcuchowa) tak, że całość jeden wielki mechanizm tworzy. Kiedy maszyna dobrze zbudowana zostaje, Bajtek jedno z kół napędzać zaczyna, tym samym w ruch wszystkie pozostałe wprawiając. Niestety mechanizmy przez chłopca wykonywane już tak wielce skomplikowane się stają, że nie każda z machin po wybudowaniu działać jest w stanie, a jest tak wtedy, gdy działanie niektórych przekładni wyklucza się wzajemnie. Chłopiec chciałby więc najprzód, to jest przed wykonaniem wiedzieć, czy dana maszyna działać będzie, czy też obmyślony system trybów jest zły i machineria ruszyć nie będzie zdolna.
Choć wszystkie koła w rozmiarach jednakie są, Bajtek, w konstrukcjach swoich, kilka rodzajów przekładni tworzyć może, gdyż każde koło z dwóch wieńców zębatych się składa, z których mniejszy jeden, a większy dwa tuziny zębów posiada. Ku temu jeszcze, przy łączeniu kół z łańcucha użyciem, ten ostatni zwyczajnie założony lub skręcony być może. Każde koło z każdym innym na wiele sposobów połączonym w przekładnie być może. O ile w trakcie budowy potrzeba taka zachodzi (np. niemożliwe jest odpowiednie kół rozmieszczenie), Bajtek, niektóre zaplanowane przekładnie zębate, przekładniami ze skręconym łańcuchem zastępuje, które skutek taki sam przynoszą. Tak więc na uwadze mieć należy, że każdą z zaprojektowanych konstrukcji zbudować można (po ewentualnych modyfikacjach wspomnianego w uprzednim zdaniu rodzaju). Zagadką jedynie to pozostaje, czy ową machinerię w ruch później wprawić się uda oraz jak żwawo i w którą stronę wybrane tryby obracać się będą?
Wejście
W pierwszej linii liczba testów (projektów maszyn) t (1 ≤ t ≤ 20).
Pierwsza linia każdego testu zawiera dwie liczby całkowite k (2 ≤ k ≤ 106) i p (k–1 ≤ p ≤ 106) oznaczające odpowiednio liczbę kół zębatych i liczbę przekładni.
W kolejnych p liniach opis każdej przekładni złożony z pięciu liczb k1, w1, k2, w2 i r, których znaczenie jest następujące:
k1 - numer pierwszego koła przekładni, w1 - numer wykorzystanego w tym kole wieńca zębatego (1 - mniejszy, 2 - większy)
k2 - numer drugiego koła przekładni, w2 - numer wykorzystanego w tym kole wieńca zębatego (wartości jak wyżej)
r - rodzaj przekładni (1 - zębata, 2 - łańcuchowa z łańcuchem założonym normalnie, 3 - łańcuchowa z łańcuchem skręconym).
Następnie liczba q (1 ≤ q ≤ 100) oznaczająca, dla ilu kół należy udzielić odpowiedzi na pytanie:
Czy to koło będzie się obracać w tym samym kierunku (zgodnym) co napędowe czy w przeciwnym?
Jeżeli dane koło będzie się obracać z inną szybkością niż koło napędowe, należy dodatkowo odpowiedzieć na pytanie:
Czy to koło będzie się obracać szybciej czy wolniej od napędowego i ile razy?
W kolejnej linii q numerów kół, których dotyczą powyższe pytania.
Koła numerowane są od 1 do k, a napędowe jest zawsze koło o numerze 1.
Wyjście
Dla każdego projektu należy w oddzielnej linii określić czy maszyna będzie działać czy nie, wypisując jedno z następujących zdań:
"TEN PROJEKT JEST DOBRY!" lub "TA MASZYNA DO RUCHU NIE JEST ZDOLNA!"
Tylko jeśli projekt maszyny jest prawidłowy, należy dodatkowo dla każdego z q kół podać w osobnej linii informację w formacie:
("zgodnie"|"przeciwnie")[", %o razy "("szybciej"|"wolniej")]
gdzie %o oznacza odpowiednią liczbę zapisaną w systemie oktalnym - ulubionym systemie liczbowym Bajtka.
Przykład
Wejście: 3 6 6 1 2 2 1 1 1 1 3 2 2 3 2 4 2 1 1 2 5 2 1 5 1 6 2 1 6 1 4 1 3 5 6 2 5 3 4 3 5 1 2 2 2 2
1 1 2 1 2
1 2 3 1 1
1 2 3 1 3
3 1 2 2 1
3
1 2 3 4 4 1 2 3 1 2 1 2 3 2 1
1 1 2 2 1
3 2 4 1 1 4 4 3 2 1
Wyjście: TEN PROJEKT JEST DOBRY! zgodnie, 2 razy wolniej przeciwnie, 2 razy szybciej przeciwnie zgodnie, 2 razy wolniej przeciwnie, 2 razy wolniej TEN PROJEKT JEST DOBRY! zgodnie zgodnie przeciwnie, 2 razy szybciej TA MASZYNA DO RUCHU NIE JEST ZDOLNA!
Pomoc do przykładu: Na rysunkach poniżej przedstawiono maszyny zbudowane według projektów opisanych na wejściu w powyższym przykładzie.
|
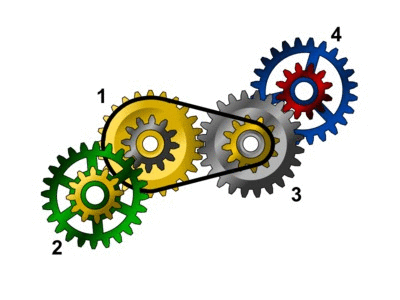
Projekt nr 1 Ten działający mechanizm można zbudować bez jakiejkolwiek modyfikacji projektu. |
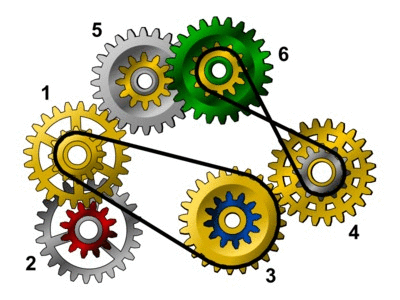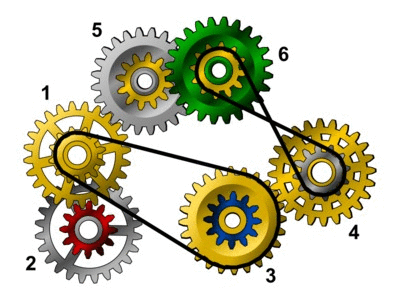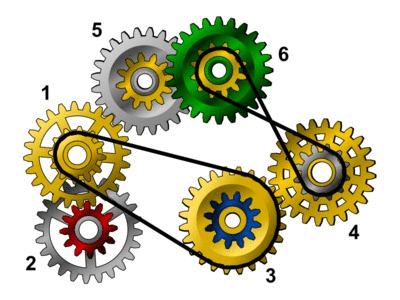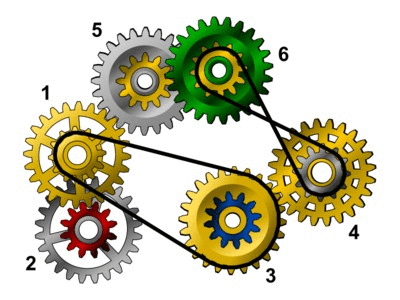 |
|
Projekt nr 2 Z projektu wynika, że koła nr 1 i 3 wchodzą w skład dwóch przekładni: zębatej i ze skręconym łańcuchem. W praktyce, nie można ich wykonać jednocześnie, tak jak to przedstawia animacja. Ponieważ jednak obie przekładnie dają taki sam efekt, Bajtek może (tak ja to opisano w treści zadania) zastąpić przekładnię zębatą przekładnią łańcuchową, odsuwając od siebie oba koła i łącząc je kolejnym skręconym łańcuchem, założonym tak samo jak ten już istniejący (brązowy na rysunku). Inaczej: w projekcie nie ma przekładni, których działanie wyklucza się wzajemnie, uznajemy więc, że mechanizm będzie działać - koła da się wprowadzić w ruch. |
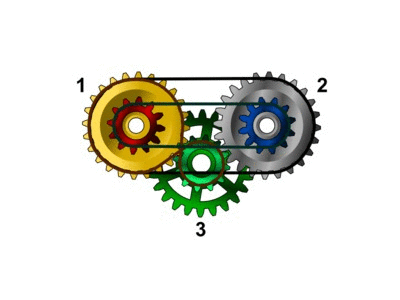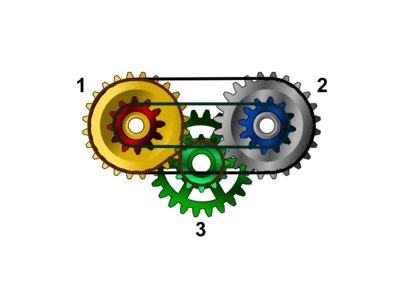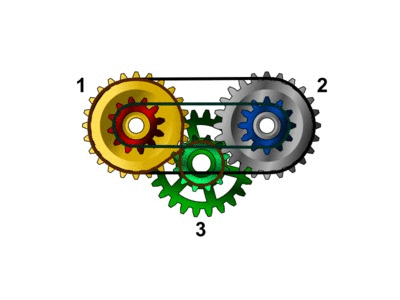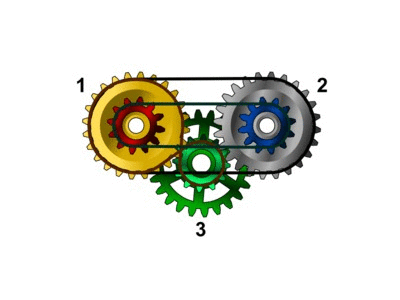 |
|
Projekt nr 3 Działanie dwóch przekładni (łańcuchowej i zębatej), w skład których wchodzą koła nr 1 i 3, wyklucza się wzajemnie. Taki mechanizm nie będzie więc działać. |
 |
| Dodane przez: | Witold Długosz |
| Data dodania: | 2013-07-25 |
| Limit czasu wykonania programu: | 1s-2s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ASM64 GOSU |
| Pochodzenie: | ALGOLIGA |
ukryj komentarze
|
2013-10-19 17:18:11 Witold D³ugosz
Mała zmiana limitów czasowych i rejudge. Zwracam wszystkim uwagę na limit rozmiaru stosu wynoszący standardowo 8MiB. Ostatnio edytowany: 2013-10-19 17:19:24 |

 RSS
RSS