| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_11_09 - Wyspa do zasiedlenia |
 Słynny podróżnik i odkrywca - Bajtolomeo Diaz, zasłużył się po raz kolejny swej ojczyźnie Bajtocji, odkrywając na dalekich wodach Algoceanu bezludną wyspę, bogatą w złoża szlachetnych kruszców. Gdy ta wspaniała wiadomość dotarła do uszu króla Bajtolomeusza Pierwszego, ten natychmiast nakazał jak najszybszą kolonizację wyspy.
Słynny podróżnik i odkrywca - Bajtolomeo Diaz, zasłużył się po raz kolejny swej ojczyźnie Bajtocji, odkrywając na dalekich wodach Algoceanu bezludną wyspę, bogatą w złoża szlachetnych kruszców. Gdy ta wspaniała wiadomość dotarła do uszu króla Bajtolomeusza Pierwszego, ten natychmiast nakazał jak najszybszą kolonizację wyspy.
W Bajtocji do określania współrzędnych geograficznych, od dawien dawna stosuje się układ współrzędnych kartezjańskich, a jednostka jest w nim tak dobrana, aby położenie wszystkich ważnych miejsc określone było parą liczb całkowitych. Tak więc nowoodkrytą wyspę możemy opisać, jako wielokąt, którego wierzchołki znajdują się w punktach kratowych.
Król Bajtolomeusz lubuje się w liczbach całkowitych, zarządził więc, aby kolonizacja wyspy polegała w pierwszym etapie na wybudowaniu nowych miast-osad we wszystkich punktach kratowych, znajdujących się w jej obrębie, w których jest to tylko możliwe. Na wyspie znajdują się bowiem trudnodostępne obszary (każdy w kształcie wielokąta), takie jak bagna, góry, jeziora itp., na których miast wybudować się nie da. Ich brzegi, jak również brzeg wyspy, też do tego się nie nadają. Liczba miejsc odpowiednich do założenia osad może się więc okazać mocno ograniczona.
Drugi etap kolonizacji będzie polegał na wysłaniu na wyspę kolonistów (ochotników) - przedstawicieli różnych zawodów, którzy zamieszkają w nowowybudowanych osadach i będą je rozwijać. Król nie narzuca pionierom, w których miastach mają się osiedlać i daje każdemu z nich możliwość (całkowicie niezależnego od innych) wyboru. Tym samym liczba możliwych sposobów kolonizacji wyspy staje się bardzo duża. I tu pojawia się problem, z którym nie mogą sobie poradzić nadworni rachmistrze króla Bajtolomeusza, a Ty musisz go rozwiązać: na ile różnych sposobów koloniści mogą zasiedlić miasta na wyspie?
Uwaga: ponieważ wynik może być ogromną liczbą, należy go podać modulo 1000000007.
Wejście
W pierwszej linii liczba wierzchołków wielokąta-wyspy n (3 ≤ n ≤ 200000).
W kolejnych n liniach po dwie liczby całkowite xi, yi (-109 ≤ xi, yi ≤ 109) oznaczające współrzędne kolejnych wierzchołków.
Następnie liczba obszarów wykluczonych z zasiedlenia k (0 ≤ k ≤ 100).
Później opis tych obszarów, z których każdy ma taką strukturę jak opis wyspy: składa się z liczby wierzchołków m (3 ≤ m ≤ 2000), a następnie z m par liczb całkowitych xi, yi (-109 ≤ xi, yi ≤ 109) oznaczających współrzędne kolejnych wierzchołków.
W kolejnej linii liczba różnych zawodów reprezentowanych przez kolonistów z (1 ≤ z ≤ 200000).
W ostatniej linii z liczb całkowitych ai (0 ≤ ai < 264) oznaczających ilu przedstawicieli wśród osadników ma każdy z zawodów.
Wielokąty opisujące wyspę i obszary nienadające się do zasiedlenia, są wielokątami bez samoprzecięć. Wszystkie obszary wykluczone z zasiedlenia znajdują się w całości wewnątrz wyspy, tzn. nie mają punktów wspólnych z jej brzegiem. Żadne dwa z tych obszarów nie mają punktów wspólnych.
Wyjście
Jedna liczba całkowita oznaczająca na ile sposobów (modulo 1000000007) koloniści mogą zasiedlić wyspę.
Uwaga 1: Jeżeli na wyspie nie ma miejsc nadających się do założenia miast, to należy przyjąć, że nie ma sposobu na zasiedlenie wyspy.
Uwaga 2: Jeżeli na wyspie są miejsca na założenie osad, ale nie ma kolonistów chętnych do jej zasiedlenia, to należy przyjąć, że jest jeden sposób kolonizacji - bez udziału osadników.
Przykład
Wejście: 5 1 1 5 1 6 3 9 5 2 9 2 4 2 4 2 8 5 7 7 5 4 5 2 5 4 4 4 2 2 3 5 2 3
Wyjście: 282475249
Rysunek do przykładu: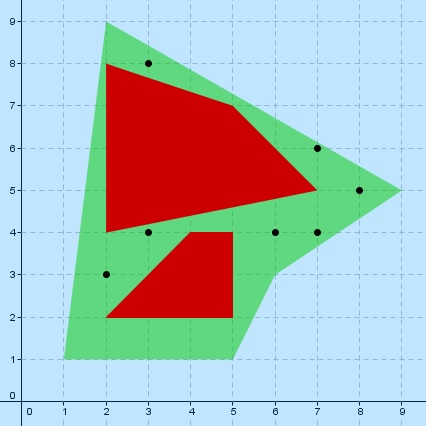 |
Na tej wyspie jest tylko siedem miejsc, w których założone zostaną osady. |
| Dodane przez: | Witold Długosz |
| Data dodania: | 2013-07-25 |
| Limit czasu wykonania programu: | 0.100s-0.400s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ASM64 GOSU |
| Pochodzenie: | ALGOLIGA |
ukryj komentarze
|
2013-10-21 22:18:38 Witold D³ugosz
Zawody utrudniają zadanie o tyle, że nie jest podana wprost liczba kolonistów. |
|
|
2013-10-20 22:26:32 Kamil Debowski
Tak patrzę teraz na outy dla testu przykładowego oraz tego od Filipa i się trochę dziwię. Mamy jakieś tam zawody tych ludzi i narzucało się założenie nierozróżnialności kolonistów tej samej profesji. A tu chyba się okazuje, że trochę inaczej trzeba całość interpretować. Czyli zawody nic nie zmieniają, czy może mają jakieś ukryte znaczenie, a ja czegoś nie widzę? |
|
|
2013-10-20 20:08:11 Mariusz ¦liwiñski
(3999999996000000001^2)%1000000007 = 50625 |
|
|
2013-10-20 20:01:12 Filip Czaplicki
Jaki jest out dla testu: 4 1000000000 1000000000 1000000000 -1000000000 -1000000000 -1000000000 -1000000000 1000000000 0 1 2 ? |
|
|
2013-10-20 19:10:23 Witold D³ugosz
Gratulacje. |
|
|
2013-10-20 16:45:41 Mariusz ¦liwiñski
:D |
|
|
2013-10-19 23:21:42 Mariusz ¦liwiñski
Tak, znalazłem zapętlenie. |
|
|
2013-10-19 23:12:54 Witold D³ugosz
Nie to jest powodem. Dostajesz TLE dla małego testu. Ostatnio edytowany: 2013-10-19 23:20:36 |
|
|
2013-10-19 22:50:27 Mariusz ¦liwiñski
Stary klaster :-) |

 RSS
RSS