| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_01_05 - Kolorowanie |
W przedszkolu dla wybitnie uzdolnionych, dzieci kolorują kółka graniaste oraz rozwiązują zagadki matematyczne. Kółko graniaste n-kąciaste to n-kąt foremny podzielony na sektory przez odcinki łączące środek okręgu wpisanego/opisanego na nim z wierzchołkami. Na rysunku poniżej przedstawione jest kółko graniaste 6-kąciaste:
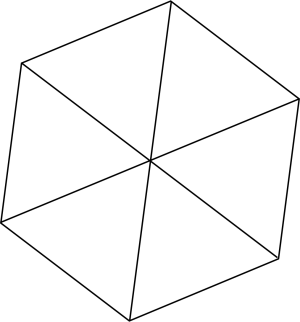
Opiekunowie rozdali dzieciom k kolorów flamastrów i kazali namalować wszystkie istotnie różne kółka graniaste n-kąciaste. Dodatkowo chcą znać ich ilość, ale jako że spodziewają się dużego wyniku, dzieci muszą go podać modulo 100003. Każdemu sektorowi kółka graniastego należy przyporządkować dokładnie jeden z k kolorów. Dwa kółka graniaste uznajemy za takie same jeśli z jednego możemy otrzymać drugie przy pewnym obrocie, bądź przewróceniu na drugą stronę (flamastry dzieci prześwitują).
Wejście
Wejście zaczyna się liczbą 1<=t<=1000 oznaczającą ilość przypadków testowych. Każdy przypadek testowy składa się z dwóch liczb, kolejno: 1<=n<=105 - liczba sektorów kółka graniastego oraz 1<=k<=1000 - liczba dostępnych kolorów flamastrów.
Wyjście
Dla każdego przypadku testowego należy wypisać w osobnej linii ilość istotnie różnych pokolorowań kółka graniastego n-kąciastego, z dokładnością do obrotów i symetrii oraz mając do dyspozycji k kolorów flamastrów, modulo 100003.
Przykład
Wejście: 5
1 2
3 2
5 2
10007 1000
20014 1000 Wyjście: 2
4
8
51307
82148
| Dodane przez: | Adam Bąk |
| Data dodania: | 2012-09-13 |
| Limit czasu wykonania programu: | 0.109s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: GOSU |
| Pochodzenie: | ALGOLIGA |

 RSS
RSS