| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
KMS_B2 - Mixture of Gaussians |
Dany jest zbiór n punktów płaszczyzny
d=((x1,y1),..., (xn,yn ))
Poszczególne punkty są od siebie wzajemnie niezależne i mają rozkład, będący mieszaniną K rozkładów normalnych, tj. mają rozkład zadany przez gęstość
p(x,y)= w1 p1(x,y)+ ... + wK pK(x,y),
gdzie w1+...+wK=1 oraz
pj (x,y)=
1/(2
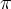 sxjsyj)
exp{ -[(x-mxj )/sxj ]2/2
-[(y-myj )/syj ]2/2
}.
sxjsyj)
exp{ -[(x-mxj )/sxj ]2/2
-[(y-myj )/syj ]2/2
}.
Parametry wj, mxj, myj oraz sxj, syj są nieznane. Zadanie polega na dobraniu tych parametrów metodą EM (Expectation-Maximization), tak aby wartość funkcji
L(d)= -ln(p(x1,y1)) - ... -ln(p(xn,yn))
była możliwie jak najmniejsza.
Wejście
W pierwszym wierszu podana jest wartość K oraz n oddzielone spacją.
W kolejnych n wierszach podane są kolejne wartości xi, yi oddzielone spacją.
Uwaga: W pierwszych dwóch zestawach K=1, czyli problem sprowadza się do metody ML.
Wyjście
W pierwszym wierszu należy podać otrzymaną wartość L(d). W następnych K wierszach należy wypisać kolejne wartości wj, mxj, sxj, myj, syj oddzielone spacjami.
Liczby wj muszą się sumować do jedności oraz żadna z liczb sxj, syj nie może być mniejsza od 10-15
Każdy z 10 testów ma indywidualny próg na wartość L(d), powyżej którego test nie jest zaliczany. Osoba, która rozwiąże wszystkie testy i otrzyma najmniejszą sumę L(d) otrzyma dodatkowe 5% (razem 10%).
Przykład 1
Wejście 2 10 5 5.5 5.5 4.5 5 4.5 4.5 5 4.9 5.1 4.7 4.9 -2 -2 -2 -2.1 -2.1 -1.9 -1.9 -2 Wyjście 0.545208 0.4 -2 0.0707107 -2 0.0707107 0.6 4.93333 0.309121 4.91667 0.348409
Przykład 2
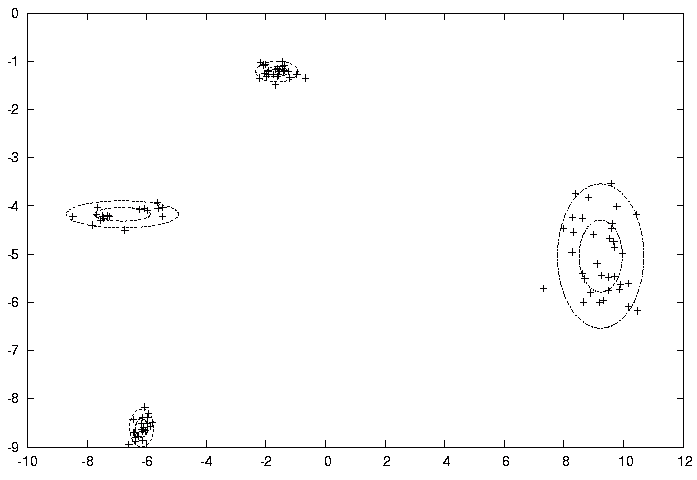
Na poniższym wykresie punkty są zaznaczone przez '+', zaś rozwiązanie jest zaznaczone w ten sposób, że średnie poszczególnych składowych leżą w środkach elips, zaś elipsy mają promienie sxj, syj oraz 2sxj, 2syj.
A po co to komu?
Opisany problem może być wykorzystywane w grupowaniu danych (clustering). Mamy punkty na płaszczyźnie i chcemy podzielić je automatycznie na K grup. Mając wyznaczone współczynniki mieszaniny rozkładów normalnych, możemy dla każdego punktu (xi,yi ) wyznaczyć prawdopodobieństwa przynależności tego punktu do j-tej składowej, czyli
wjpj (xi, yi) / p (xi, yi)
W ten sposób otrzymujemy rozmyte grupowanie danych.
Odnośniki
- Wykład o metodzie ML
- Wykład z modelowania internetu, str. 24-28.
- Applet dla problemu Mixture of Gaussians w nieco bardziej skomplikowanej formie.
- Wikipedia.
- Google.
| Dodane przez: | Adam Nadolski |
| Data dodania: | 2006-11-26 |
| Limit czasu wykonania programu: | 1s-1.053s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ERL GOSU JS-RHINO NODEJS PERL6 VB.NET |
